Integrální kriterium
Pojmenování funkčního bloku
Lib.Mervis.v1_0.IntegralCriterion
Popis
Pomocný blok sloužící pro výpočet kladného a záporného integrálu rozdílu dvou hodnot (např. žádané a skutečné hodnoty). Těchto integrálu se pak využívá v optimalizačních úlohách složitejších funkčních bloků.
Potřebné reference projektu
- Lib.Mervis
Použití v ST
program test
var
ic: lib.mervis.v1_0.IntegralCriterion;
end_var
ic();
end_program
Popis vstupů a výstupů
| Vstupy | Jméno | Datový typ | Retain | Nutno připojit | Význam |
| Input | real | Ne | Ano | Skutečná hodnota | |
| SetPoint | real | Ne | Ano | Žádaná hodnota | |
| CanAttach | bool | Ne | Ano | Povoluje možnost povelu na přidání | |
| CanDettach | bool | Ne | Ano | Povoluje možnost povelu na odebrání | |
| Diff | real | Ne | Ne | Určuje pásmo necitlivosti okolo žádané hodnoty (toto pásmo je od -Diff/2 do Diff/2) | |
| LimitForAttach | real | Ne | Ne | Limitní hodnota kladného integrálu pro povel na přidání | |
| LimitForDettach | real | Ne | Ne | Limitní hodnota záporného integrálu pro povel na odebrání |
| Výstupy | Jméno | Datový typ | Význam |
| AttachCmd | bool | Povel pro přidání (aktivní po dobu jednoho cyklu) | |
| DettachCmd | bool | Povel pro odebrání (aktivní po dobu jednoho cyklu) |
| Metody bloku | Jméno | Význam |
| Restart | Slouží pro vynulování interních hodnot a restartu výpočtu |
Podrobný popis funkce
Základní částí bloku je výpočet rozdílu SetPoint (žádaná) - Input (skutečná). Tento rozdíl poté vstupuje na dva integrátory, první slouží pro integraci kladného rozdílu (žádaná větší než skutečná) - budeme ho označovat jako kladný integrál. Druhý slouží pro integraci záporného rozdílu (žádaná menší než skutečná) - budeme ho označovat jako záporný integrál.
Pro vyloučení zákmitů je okolo žádané hodnoty vytvořeno pásmo necitlivosti o velikosti Diff (SetPoint - Diff/2 až SetPoint + Diff/2). Pokud se skutečná hodnota nachází v tomto pásmu nedochází k žádné integraci a výstupy obou integrátorů jsou nastaveny na nulovou hodnoty. Jakmile se skutečná hodnota dostane mimo toto pásmo, dojde k integraci příslušným integrátorem:
- skutečná hodnota je menší než žádaná zmenšená o Diff/2 - zvětšuje se kladný integrál, záporný zůstává nulový
- skutečná hodnota je větší než žádaná zvětšená o Diff/2 - zvětšuje se záporný integrál, kladný zůstává nulový
V každém kroku se porovnávají aktuální výstupy obou integrátoru s limitními hodnotami - kladný integrál s LimitForAttach, záporný s LimitForDettach, pokud v některém případě dojde k prekročení těchto limitů a současně má odpovídající vstup CanAttach/CanDettach stav true, dojde k aktivaci příslušného výstupu AttachCmd/DettachCmd a následnému vynulování integrálu. Tím je blok připraven k dalšímu cyklu. Tím, že se limitní hodnoty porovnávají s hodnotou integrátoru mají tyto daný fyzikální význam - jejich rozměr je dán jednotkou řízené veličiny a časem - ten se počítá v minutách, výsledná jednotka tedy může být např °C . min.
Pro názornou představu lze uvést, pokud bude limit nastaven na hodnotu 60 znamená to, že k aktivaci výstupu AttachCmd dojde po 60 minutách když je skutečná hodnota 1°C pod pásmem necitlivosti a nebo po 1 minutě když je skutečná hodnota 60°C pod pásmem necitlivosti - musí platit rozdíl_ve_stupních x čas_v_minutách se rovná 60
K názornému pochopení slouží následující obrázek:
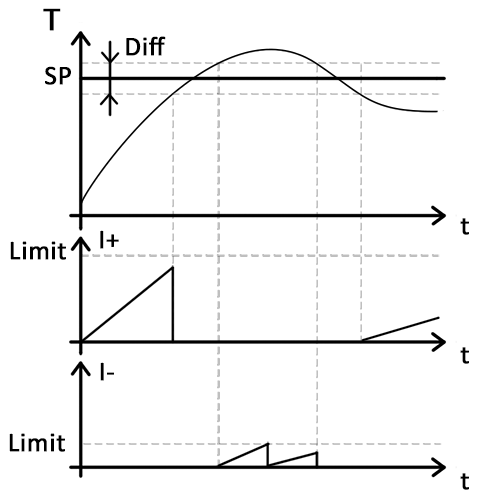
Vysvětlivky grafu - V prvním grafu je průběh regulované veličiny, SP = SetPoint, Limit = patřičná hodnota limitu - LimitForAttach/LimitForDettach
Tento obrázek lze rozdělit na pět částí
- Část 1
Skutečná hodnota je menší než žádaná ⇒ roste kladný integrál
- Část 2
Než stihl kladný integrál překročit limitní hodnotu, vstupuje skutečná hodnota do pásma necitlivosti a dochází k vynulování integrálů
- Část 3
Skutečná hodnota je větší než žádaná ⇒ roste záporný integrál, ve chvíli kdy překročí limitní hodnotu nastaví se na jeden cyklus výstup DettachCmd a následně se vynuluje, skutečná hodnota je ale stále vyšší, proto integrál opět narůstá
- Část 4
Skutečná hodnota se opět dostává do pásma necitlivosti ⇒ dochází k vynulování integrálu
- Část 5
Opakuje se situace z první části